Affiliation:
Department of Chemistry and Biochemistry, Old Dominion University, Norfolk, VA 23529, USA
Email: jwlee@odu.edu
ORCID: https://orcid.org/0000-0003-2525-5870
Explor Neurosci. 2025;4:100685 DOI: https://doi.org/10.37349/en.2025.100685
Received: December 16, 2024 Accepted: March 17, 2025 Published: April 26, 2025
Academic Editor: Dirk M. Hermann, University of Duisburg-Essen, Germany
Aim: This study is to better understand how the transient ion transport activity of touch receptors could change the graded potential to stimulate an action potential firing.
Methods: The latest transmembrane-electrostatically localized protons/cations charges (TELC) theory is employed for numerical analysis to calculate the neural touch signal transduction responding time required to fire an action potential spike.
Results: A neural action potential spike was constructed successfully using newly developed time-dependent TELC-based neural transmembrane potential integral equations (Equations 5, 6, and 7). The results explicated that the TELC curve has an inverse relationship with neural transmembrane potential since its curve appears as an inverse mirror image to the action potential spike. Based on the TELC density at resting membrane potential of –70 mV calculated to be 3,900 (excess protons + cations) per μm2 and that at the stimulation threshold level (–55 mV) calculated to be 3,100 (excess protons + cations) per μm2 on extracellular membrane surface, the neural touch signal transduction responding time from PIEZO channel ion conduction to reduce the TELC density to the stimulation level of 3,100 TELC per μm2 has now, for the first time, been calculated for action potential firing.
Conclusions: The activity of a single or a few PIEZO channels may be sufficient to generate a “graded potential” to trigger an action potential spike firing. With a high number (200–300) of PIEZO channels activated by touch, it can generate the required “graded potential” to reach the stimulation threshold level (–55 mV) within a neural touch signal transduction time as fast as 0.3 ms. The calculated neural touch signal transduction responding time (e.g., 0.3 ms) may have fundamental implications not only for neuroscience but also for other science and technology fields such as bioengineering and sports physiology.
The 2021 Nobel Prize in Physiology or Medicine was recently awarded to David Julius and Ardem Patapoutian “for their discoveries of receptors for temperature and touch” [1]. It is now well established that touch receptors provide sensory inputs to inform the brain about objects in our environment. Touch sensation is vital for survival and, without it, even simple activities such as feeding, dressing, or standing would be exceedingly difficult to accomplish. Like in hearing [2], balance, and proprioception, the sensing of a touch is initiated by mechanosensory receptor cells [3–5]. Mechanosensitive membrane proteins [6–8] are known to be essential for tissue development, cellular motion, osmotic homeostasis, and sensing external and self-generated mechanical cues like those responsible for touch and proprioception. These cells contain mechanotransduction channels (such as PIEZO) [9–11], which convert physical stimuli to membrane potential changes, called receptor potentials, which could trigger neuronal action potential spikes. These action potentials are transmitted by sensory afferents to the brain, where sensory percepts are formed. Although the mechanism and site of transduction across end organs remain unclear, Piezo2 has emerged as the prominent mechanosensitive channel involved in light touch [12, 13]. Membrane potential response has been recorded from a Neuro2A (N2A) cell under current clamp to mechanical stimulation of PIEZO generated by depressing a glass probe against the cellular membrane [14]. Although much of the structural and mechanistic principles underlying Piezo gating and its general roles in physiology have been well elucidated through more than a decade of intense research, a knowledge gap still exists [15–17]. For example, exactly how the transient ion transport activity of touch receptors could physically change the graded transmembrane potential and stimulate the firing of action potential spikes was still not entirely clear. What is the neural touch signal transduction responding time from the moment of “touch” to the time needed to change a graded transmembrane potential from the resting level (–70 mV) to the stimulation threshold level (–55 mV) to fire an action potential spike? This is a fundamental scientific question that needs to be answered.
Recently, through our neuroscience study [18, 19] based on the transmembrane-electrostatically localized protons (TELP)/cations charges (TELC) model, which is also known as the “TELP theory” in protonic bioenergetics [20–25], the neural resting and action potential has better been elucidated as the voltage contributed by TELC at a liquid-membrane interface in a neuron “localized protons/cations-membrane-anions capacitor” system. This TELC-based new understanding of transmembrane potential can help to better elucidate exactly how the transient ion transport activity of touch receptors could physically stimulate the firing of action potential spikes at a bioenergetics level.
The TELC-based approach is complementary to the pioneering work of Hodgkin and Huxley [26] where membrane capacitor and transmembrane ion current were also considered [19], which is in line with the present study with TELC. However, probably due to the subtlety of the TELC theory and due to the complexity of the neural system and its associated energetics, currently, not necessarily everyone could easily understand the TELC-based neural transmembrane potential theory and its implications [18]. For example, Silverstein [27] previously presented his critique on the TELC model [18]. The author (Lee) welcomes critiques and discussions as that can also be a part of the process for scientific progress and learning. As we recently discussed in a review article published in the current trends of neurology [19], Silverstein’s critiques [27, 28] actually were largely stemmed from his own errors or misunderstandings of the TELC model [29]. In the present article, readers will find that the TELC model is incredibly useful to enable a better fundamental understanding of neuroscience including the elucidation of neural stimulation by touch and the calculation of neural touch responding time for the first time.
The TELC-based neural transmembrane potential theory [18] is built on the knowledge that liquid water can serve as a protonic conductor (Figure 1A), which well agrees with the fact that protons can use the “hops and turns” mechanism and quickly translocate among water molecules as first outlined by Grotthuss [30–33] who developed this model to explain the enormous mobility of the H+ ion relative to other ions. As reported previously [18], this protonic conduction (Figure 1A) “is much faster than the diffusive movement of a non-proton cation such as Na+ which tightly binds with water molecules. For a non-proton cation to move through liquid water, it must carry its bound water molecules and physically plough through the molecular array of liquid water”. Consequently, protonic conduction is much faster than the movement of non-proton cations such as Na+, K+, and Mg2+.
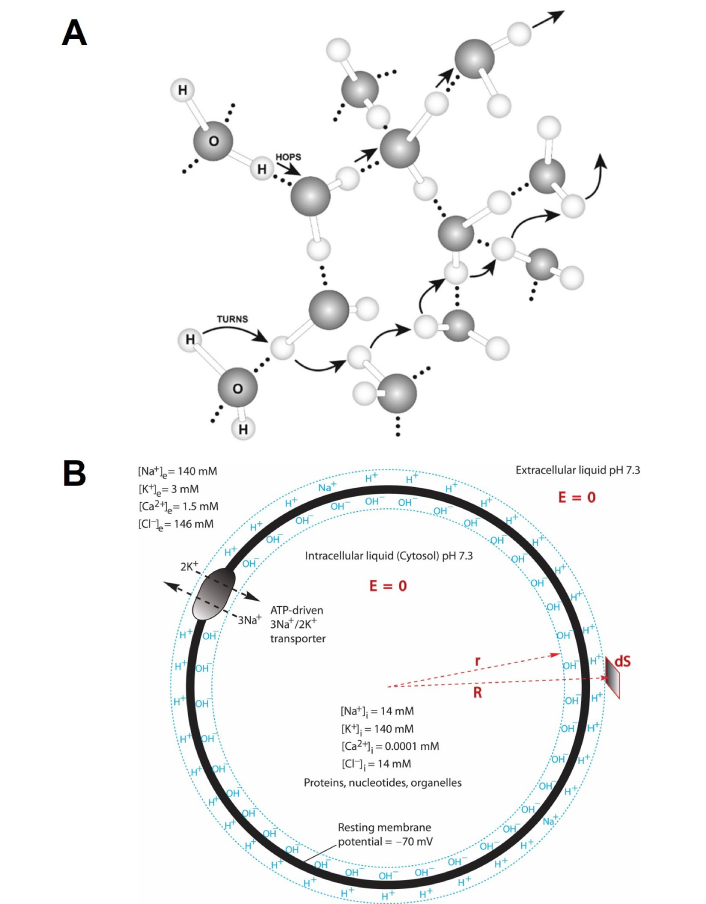
Illustration of liquid water as a protonic conductor in relation to neural membrane capacitor formation. (A) Protons can quickly transfer among water molecules by the “hops and turns” mechanism (also known as the Grotthuss mechanism [33]) so that a microscopic water body may be thought of as a protonic conductor; (B) illustration of adenosine triphosphate (ATP)-driven sodium/potassium (3Na+/2K+) pump in relation to transmembrane-electrostatically localized protons/cations charges (TELC) capacitor formation in a neuron: an ATP-driven sodium/potassium (3Na+/2K+) pump transporting 3 sodium cations across the cytoplasmic membrane from inside the cell to the outside while co-transporting 2 potassium cations across the membrane from the outside into the cell, which results in a transmembrane-electrostatically localized protons/cations-neural membrane-anions capacitor as illustrated by the TELC at the liquid-membrane interface along the extracellular side while localized anions along the intracellular side. “E = 0” means the electric field in the liquid is zero. “R” and “r” are polar coordinates. “dS” is a surface differential element. The extracellular and intracellular bulk-liquid phase Na+, K+, Cl–, Ca2+ concentrations shown in the drawing are based on Ref. [34]
Note. Adapted from “Proton-Electrostatics Hypothesis for Localized Proton Coupling Bioenergetics” by Lee JW. Bioenerg. 2012;1:104 (https://doi.org/10.4172/2167-7662.1000104). CC BY.
According to the TELC action potential theory [18, 19], as illustrated in Figure 1B, an adenosine triphosphate (ATP)-driven sodium/potassium (3Na+/2K+) pump transports every 3 sodium cations across the neuron cytoplasmic membrane from inside the cell to the outside while co-transports every 2 potassium cations across the membrane from the outside into the cell per ATP consumption. Two of the 3 sodium cations transported out of the cell are charge-balanced by the 2 potassium cations transported into the cell whereas one of the 3 sodium cations (positive charges) is not charge-balanced, becoming an excess (extra) positive charge at the extracellular side. Consequently, this 3Na+/2K+ transport process per ATP consumption results in a net translocation of one positive charge (e.g., Na+) across the cytoplasmic membrane from inside the neuronal cell to the outside leaving its countering anion (e.g., Cl–) inside the cell. As the 3Na+/2K+ transport process continues, it results in the accumulation of excess positive charges (cations) outside the neuron cell while accumulating excess anions (negative charges) inside the cell, in addition to setting up the initial ion concentration gradients [34] of Na+ (high outside), K+ (high inside), and indirectly, Cl– (high outside). By “excess cations” (or excess positive charges), it means that their positive charges are not balanced by their countering anions within the same liquid phase since their countering anions (excess negative charges) are on the other side of the membrane. The excess positive charges and the excess negative charges across the neural membrane will form a TELC capacitor (Figure 1B) which follows the principle of total charge neutrality.
During TELC capacitor formation, any transmembrane-electrostatically localized excess non-proton cations may be exchanged out by the protons from the liquid phase. As reported previously [18, 19], “any excess cations that are exchanged out of the TELC layer into the bulk-liquid phase will fully interact (such as hydration) with water molecules and electrostatically repel protons (parts of water molecules) from the bulk aqueous phase through the ‘hops and turns’ mechanism to the neural liquid-membrane interface to be transmembrane-electrostatically localized there along the outside surface of the neuron cell membrane where the localized protons transmembrane-electrostatically attract the excess anions such as hydroxide anions at the other side of the cell membrane” as illustrated in Figure 1B.
Since action potential is measured typically from an electrode of reference outside a neuronal cell to a measuring electrode inside the cell, its reference orientation (the n-side minus the p-side) [35, 36] is opposite to the standard Mitchellian protonic bioenergetics reference frame for the transmembrane potential Δψ (the p-side minus the n-side). Therefore, based on the TELC theory [18, 19], the neural transmembrane potential (V) including the neural resting and action potential may be mathematically expressed in relation to the TELC which is the sum of the steady-state TELP and transmembrane-electrostatically localized non-proton cations concentrations
where S is the neural extracellular membrane surface area; C is the neural membrane capacitance; l is the thickness of TELC layer; F is the Faraday constant;
Consequently, as shown in the TELC transmembrane potential equation (Equation 1), it is the TELC density
In this article, we will apply the TELC-based action potential theory (Figures 1 and 2) including the TELC neural transmembrane potential equations (Equations 1–7) to better elucidate how the transient ion transport activity of touch receptors (PIEZO) can stimulate the firing of an action potential spike in a mechanosensory receptor cell such as N2A. The neural touch signal transduction responding time from the moment of “touch” to the time needed to change a graded transmembrane potential from the resting level (–70 mV) to the stimulation threshold level (–55 mV) to fire an action potential spike will be calculated, for the first time, by application of the TELC model [18, 19]. This work enables a better understanding of neural transmembrane potential and neural stimulation by touch in firing of an action potential spike. Calculation of neural touch signal transduction responding time may have fundamental implications not only to neuroscience but also to other science and technology fields such as bioengineering and sports physiology where how fast a human could sense a touch or hear a sound could be fundamentally important.
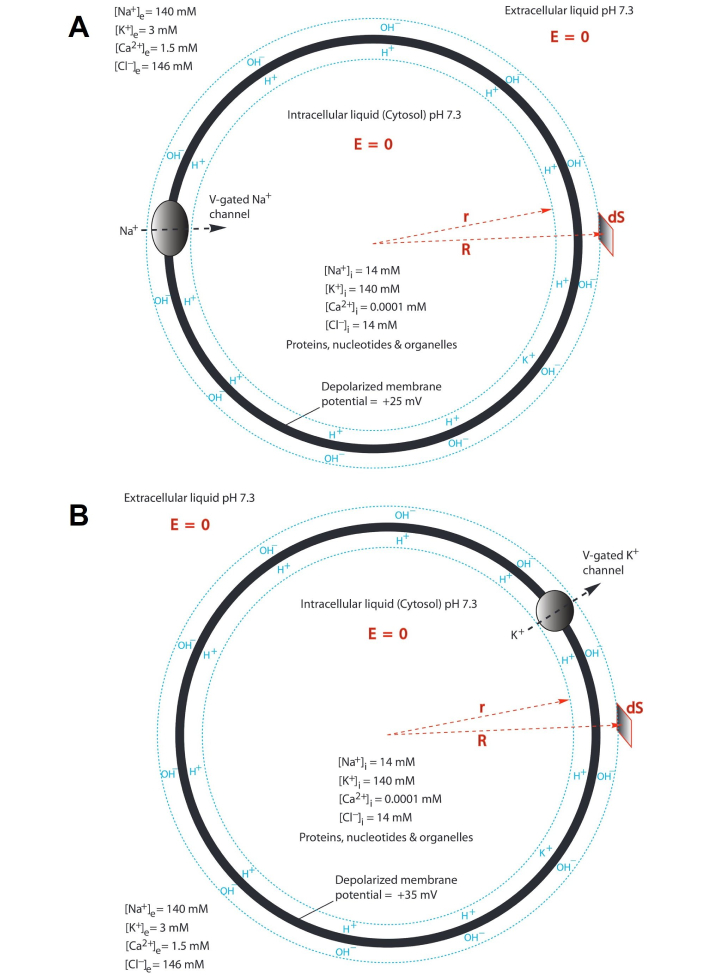
Illustration of protonic capacitor in relation to action potential in a neuron (“E = 0” means the electric field in the liquid is zero. “R” and “r” are polar coordinates. “dS” is a surface differential element. The extracellular and intracellular bulk-liquid phase Na+, K+, Cl–, Ca2+ concentrations shown in the drawings are based on Ref. [34]). (A) An opening of V-gated sodium (Na+) channels is triggered, resulting in the flow of the excess Na+ cations from the outside into the neuron cell so that the transmembrane-electrostatically localized protons/cation population density is dramatically reduced until becoming a state of “depolarization” as illustrated by the localized protons/cations at the liquid-membrane interface along the cytoplasmic (intracellular) side while anions at the liquid-membrane interface along the periplasmic (extracellular) side; (B) when the “depolarization” process reaches the membrane potential level of about +30 mV, the V-gated potassium (K+) channels open to allow the K+ cations to flow out of the neural cell resulting in a rapid “repolarization” followed by a “undershoot” and then the activities of the leaky channels with adenosine triphosphate (ATP)-driven sodium/potassium (3Na+/2K+) pumps will equilibrate and re-establish the polarized state with a resting potential as commonly observed in a neuron as shown in Figure 1B
The methods of numerical analyses employed in the research work reported here are based on the recently developed TELC action potential theory [18, 19]. Briefly, based on the neural transmembrane potential equation (Equation 1), the molar concentration of total TELC, which are the sum of the TELP and non-proton cations
where S is the neural extracellular membrane surface area; l is the TELC layer thickness; F is the Faraday constant; C is the neural membrane capacitance; and V is the neural transmembrane potential.
Using a given TELC concentration [TELC] with extracellular membrane surface area (S) and TELC layer thickness (l), the TELC surface population density was calculated as the amounts (numbers) of TELC per extracellular membrane surface area (S) (or per cell) according to the following equation:
where NA is the Avogadro constant (6.02205 × 1023 mol–1).
The TELC numbers essentially represent the localized excess proton and cation charge population density per surface area (S). From here, one also quite clearly understands that it is the localized excess proton and cation charges (but not the bulk-liquid-phase ion concentrations) that physically form the instant transmembrane potential through the membrane capacitor effect as expressed in Equations 1–3.
Based on the understanding of TELC action potential theory [18, 19], the TELC density change per cell surface area (S) because of an ionic flow across the neuronal membrane (such as the PIEZO-channel cationic conduction current) was calculated using the following equation:
where I is the time-dependent transmembrane ion current including the PIEZO-channel cationic-conduction current in Amps across the neuronal membrane; t represents time such as the PIEZO-channel cationic-conduction time; e is the elementary charge (1.60219 × 10–19 C); and S is the neuronal extracellular membrane surface area.
According to the understanding of the TELC action potential theory [18, 19], the time-dependent transmembrane-electrostatically localized charge density (TELCt) with PIEZO by touch was mathematically described by the following integration equation:
where S is the extracellular membrane surface area; F is the Faraday constant; NA is the Avogadro constant; I(t) is the net time-dependent transmembrane channel ion conduction current (in Amps), which has a positive sign when cation flows out of the cell (negative sign when cation flows into the cell); and TELC0 is the initial TELC surface density at time t = 0.
Conversely, the time-dependent membrane potential (Vt) was mathematically described by the following integral equation:
where C is the membrane capacitance and V0 is the initial membrane potential at time t = 0.
Note, the net real-time transmembrane ion conduction current [I(t)] is the summation of all the time-dependent transmembrane ion currents including (but not limited to) the time-dependent PIEZO-enabled cation conduction [IPIEZO(t)] as stimulation current, the time-dependent sodium current [INa(t)] from V-gated sodium channels, the time-dependent potassium current [IK(t)] from the V-gated potassium channel, and the time-dependent other ions currents [Il(t)] such as chloride current from certain Cl– channels, and/or the miscellaneous “leaky currents”. Therefore, real-time neural transmembrane potential (Vt) was described further by the following integral equation:
The experimental methods and materials in regard to the Coste et al. 2010 published experimental results (that are cited and presented in our article here) are reported in Ref. [9].
Table 1 lists the TELC surface population density as calculated through Equations 1–3 in relation to the resting potential (–70 mV), stimulation threshold (–55 mV), and action potential peak level (about +30 mV) in a neural cell such as N2A using specific membrane capacitance C/S of 9.2 mf/m2 based on measured experimental data [37]. At the resting neural membrane potential of –70 mV, TELC density on extracellular membrane surface is now calculated to be 3,900 (excess protons + cations) per μm2 while equal amount (3,900 per μm2) of transmembrane-electrostatically localized anions charges (negative charges) on cytoplasmic membrane surface. At the stimulation threshold level (–55 mV), the extracellular membrane surface typically has a TELC density of 3,100 (excess protons + cations) per μm2 while the cytoplasmic membrane surface has 3,100 localized (excess) anions per μm2.
The numbers of transmembrane-electrostatically localized protons/cations charges (TELC) per μm2 of membrane surface area or per cell computed from the resting membrane potential, stimulation threshold, and action potential peak level in a typical ellipsoidal Neuro2A (N2A) cell with a cell volume of 2,700 μm3 and extracellular membrane surface area of about 1,000 μm2, using specific membrane capacitance C/S of 9.2 mf/m2 based on measured experimental data [37]
| Neural membrane potential | TELC per μm2 on extracellular membrane surface | TELC per μm2 on cytoplasmic membrane surface | TELC per cell on extracellular membrane surface | TELC per cell on cytoplasmic membrane surface | |
|---|---|---|---|---|---|
| Resting potential level | –70 mV | 3,900 excess protons + cations | 3,900 excess anions | 3,900,000 excess protons + cations | 3,900,000 excess anions |
| Stimulation threshold level | –55 mV | 3,100 excess protons + cations | 3,100 excess anions | 3,100,000 excess protons + cations | 3,100,000 excess anions |
| Action potential peak level | +30 mV | 1,700 excess anions | 1,700 excess protons + cations | 1,700,000 excess anions | 1,700,000 excess protons + cations |
This is a significant result since it shows that a neural transmembrane potential change from the resting potential (–70 mV) to the stimulation threshold level (–55 mV) requires a change of TELC density by –800 charges (excess protons + cations) per μm2 from 3,900 to 3,100 TELC per μm2 on the extracellular membrane surface to induce the firing of an action potential spike.
The TELC surface density data shown in Table 1 can be quite useful to better understand neural stimulation and action potential. For a neuronal cell with a given size, the number of TELC per cell can now be calculated from the TELC surface density when its extracellular membrane area is known. For example, a total extracellular membrane surface area of about 1,000 μm2 was calculated for an ellipsoidal N2A cell with a cell volume of about 2,700 μm3 from its long and short axes of 24 μm and 18 μm and its height of 12 μm corresponding well to known dimensions of neuronal cells [38]. With the total extracellular membrane surface area for a given cell, the total TELC numbers can now be calculated on per cell basis.
Table 1 presents the total numbers of TELC per cell calculated in relation to the resting membrane potential (–70 mV), the stimulation threshold level (–55 mV), and the action potential peak level (+30 mV) for a typical N2A cell with a cell volume of 2,700 μm3 and with extracellular membrane surface area of 1,000 μm2. The calculated result listed in Table 1 shows, for the first time, that there are 3,900,000 TELC (excess protons + cations) on extracellular membrane surface per N2A cell at the resting membrane potential of –70 mV. This amount of excess positive charges (3,900,000 TELC per cell) at the membrane-liquid interface at the extracellular membrane side is electrostatically balanced by an equal amount (3,900,000 excess anions per cell) of excess negative charges (excess anions) on the intracellular membrane surface.
The result (Table 1) numerically shows the neuronal membrane system as excess positive charges (protons, cations)-membrane-excess negative charges (anions) capacitor. This also shows that, for a neural cell like a typical N2A cell to generate a resting membrane potential of –70 mV, it requires its ion-transporting activities such as the ATP-driven sodium/potassium (3Na+/2K+) pumps (Figure 1B) to translocate 3,900,000 excess positive charges (such as Na+) across the cell membrane to the extracellular liquid, while leaving 3,900,000 of excess anions (negative charges) at the intracellular side.
This result (Table 1) also reveals that, to generate a resting membrane potential of –70 mV in a neuron like a typical N2A cell, if through the ATP-driven sodium/potassium (3Na+/2K+) pump activity (Figure 1B), it may require a consumption of about 3,900,000 ATP molecules per cell. This is based on our understanding [18] that to create a pair of excess positive and negative charges across a neuronal membrane through the ATP-driven sodium/potassium (3Na+/2K+) pump requires the consumption of one ATP molecule. Therefore, we have now, for the first time, calculated the ATP consumption requirement of 3,900,000 ATP molecules per cell for transmembrane potential generation in a typical neural cell like N2A, which may have implications in bettering the fundamental understanding of neuroscience.
According to the TELC neural transmembrane potential theory [18], the 3,900,000 excess positive charges (protons and cations) per cell are transmembrane-electrostatically localized to the liquid-membrane interface along the extracellular membrane surface in a mirror image with the 3,900,000 excess negative charges (anions) per cell on the other side of the membrane. The thickness of TELC layer was previously estimated to be about 1 nm [18]. Use of the TELC action potential equations (Equations 1–3) with a TELC layer thickness of 1 nm can translate the 3,900,000 TELC (protons + cations) per cell to the effective TELC (excess protons + cations) concentration of 6.5 mM at the liquid-membrane interface along the extracellular membrane surface at a resting membrane potential of –70 mV in a neuron like a typical N2A cell.
As illustrated in Figure 1B, the extracellular liquid (pH 7.3) typically contains 140 mM Na+, 3 mM K+, 1.5 mM Ca2+, and 146 mM Cl– while the intracellular liquid (pH 7.3) typically has 14 mM Na+, 140 mM K+, 0.0001 mM Ca2+, and 14 mM Cl– (plus proteins, nucleotides, and organelles that carry substantial amounts of negatively charged groups) [34]. A transport of 3,900,000 excess positive charges (such as Na+ across the membrane), for example, by the ATP-driven sodium/potassium (3Na+/2K+) pump, would cause a minor change in Na+ concentration in the intracellular liquid by only 2.4 μM which is negligible to the 14 mM Na+ in the intracellular liquid and that is also negligible to the 140 mM Na+ in the extracellular liquid. This is consistent with the understanding of the TELC action potential theory [18] that neural transmembrane potential including the resting transmembrane potential (–70 mV) and action potential is not an immediate effect of the bulk-liquid-phase ions (such as Cl–, Na+, and K+) concentrations per se; it is just a behavior of the TELC capacitor formation from the excess positive charges and excess negative charges at the two sides of the membrane as a result of neural transmembrane ion transport activities.
To change the transmembrane potential as “graded potentials” from the resting membrane potential (–70 mV) to the stimulation threshold level of –55 mV in a neuronal cell, the excess positive charges (TELC) density at the extracellular membrane surface needs to be reduced by a change of 800,000 from 3,900,000 to 3,100,000 TELC per cell. This is an upper limit estimate since it assumes the transmembrane potential equilibrated instantly through the entire cell. For action potential firing and propagation along a myelinated axon, it may require a “graded potential” only at a small specific area of neuronal membrane such as at an axon hillock (the initial segment of an axon) or a node of Ranvier to reach the stimulation threshold level (–55 mV, equivalent to the TELC density of 3,100 excess protons + cations per μm2 on extracellular membrane surface) to fire an action potential spike. Therefore, it is entirely possible for a reduction of excess charges of less than 800,000 TELC per cell to induce a transmembrane potential spike. Anyhow, a transport of 800,000 excess positive charges such as Na+ through PIEZO channels across the membrane into the intracellular side would increase the cytoplasmic Na+ concentration by only 0.5 μM, which is negligible to the 14 mM Na+ in the intracellular liquid and negligible also to the 140 mM Na+ in the extracellular liquid.
In firing an action potential spike to raise the neuronal transmembrane potential from the stimulation threshold level (–55 mV, equivalent to the TELC density of 3,100,000 excess protons/cations per cell) at the polarized state to the depolarized state with an action potential peak level of about +30 mV (the negative charge density of 1,700,000 excess anions per cell on extracellular membrane surface), it may maximally require a change of 4,800,000 TELC per cell on extracellular membrane surface according to the data in Table 1. That is, 4,800,000 net positive charges (such as Na+) per cell may have to pass across the neural membrane from the extracellular liquid into the neuron as shown in Figure 2A to raise its transmembrane potential from –55 mV to +30 mV. This is also likely to be a theoretical upper limit estimate of TELC change since it assumes the transmembrane potential equilibrated instantly through the entire cell.
Anyhow, the 4,800,000 Na+ of TELC per cell that flow through the V-gated sodium (Na+) channels from the extracellular liquid into the neuron would raise the cytoplasmic Na+ concentration by 2.9 μM, which is again negligible to the 14 mM Na+ in the intracellular liquid and negligible also to the 140 mM Na+ in the extracellular liquid. It is now quite clear that the excess cations and excess anions which form the protons/cations-membrane-anions capacitor (thus forming TELC) constitute the transmembrane potential including action potential. Therefore, in comparing with the amounts of bulk-liquid-phase ions (charge balanced), the number of excess cations and excess anions (that form the TELC membrane capacitor giving rise to neural transmembrane potential including both the resting and action potential) are so small that their population change during a typical action potential spike has negligible impact on the concentrations of bulk-liquid-phase ions in both the intracellular liquid and the extracellular liquid; although the difference in the bulk-liquid-phase ions concentrations between the intracellular liquid and the extracellular liquid is part of the driving force for the ions channel conduction across the membrane.
We also understand, an action potential firing can occur at a small local membrane area such as at a cell membrane spot near its axon (axon hillock, and/or nodes of Ranvier in myelinated axon), sending the action potential signal down the axon. Therefore, an action potential spike may occur with a change of excess charges of substantially less than 4,800,000 TELC per cell as well. This agrees with the understanding that local transmembrane potentials that are generated usually in neuron’s dendrites can accumulate and reach the trigger zone (axon hillock) of the neuron. The trigger zone depolarizes in responding to a stimulation threshold that in turn induces an action potential spike. The action potential is propagated down the axon to the axon terminal. Anyhow, the excess cations and excess anions that form the protons/cations-membrane-anions capacitor as part of action potential activities will not cause any major change in any of the intracellular and extracellular bulk-liquid-phase ions concentrations which are typically maintained by the ATP-driven sodium/potassium (3Na+/2K+) pump and other regulated ion-transporting systems.
According to the understanding of the TELC action potential theory as illustrated in Figure 3, since the mechanically-activated PIEZO channel allows only cations (Na+/Ca2+) but not their companying anions to pass through, its activity will result in an increase of excess cations at the intracellular side and an increase of excess anions at the extracellular side. Consequently, the PIEZO-resulted excess cations will electrostatically neutralize the excess negative charges (such as OH–) at the intracellular side while the PIEZO-resulted excess anions will neutralize the excess positive charges (such as H+) at the extracellular side. This in turn will reduce the TELC density, thus modulating the neural transmembrane potential as a “graded potential” to a higher level that may be high enough (such as –55 mV) to trigger a firing of action potential spike.
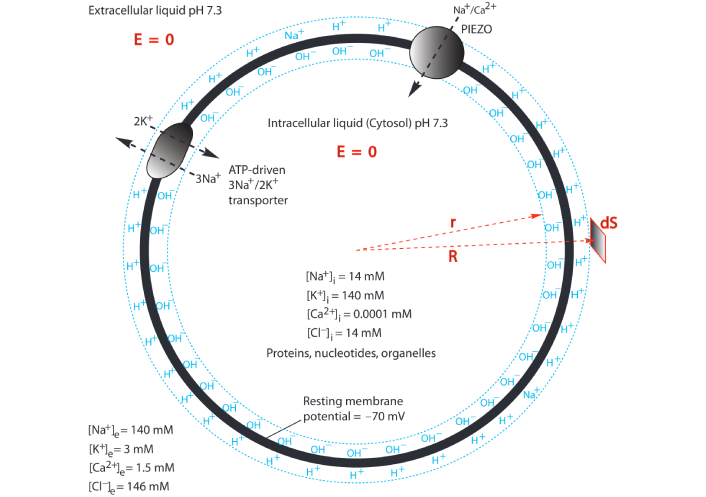
Modulation of transmembrane-electrostatically localized protons/cations charges (TELC) for neural stimulation through PIEZO by touch. “E = 0” means the electric field in the liquid is zero. “R” and “r” are polar coordinates. “dS” is a surface differential element. The extracellular and intracellular bulk-liquid phase Na+, K+, Cl–, and Ca2+ concentrations shown here are based on Ref. [34]. ATP: adenosine triphosphate
The pioneering work of the Patapoutian team has well demonstrated PIEZO as a mechanically-activated cation channel in N2A cells [9]. The mechanically-activated PIEZO channel transiently conducts cations across the neuronal plasma membrane for an example to allow Na+ (and/or Ca2+) to flow into an N2A cell. Technically, Piezo1 can selectively conduct cations, such as Na+, K+, Ca2+, and Mg2+, with a slight preference for Ca2+ [9]; and Piezo2 has the property of non-selective cationic conductance [9]. At a resting transmembrane potential of –70 mV with the extracellular and intracellular bulk-liquid phase ion concentrations as shown in Figure 3, the inward cation motive force for Na+, K+, and Ca2+ were calculated to be 130 mV, –33 mV, and 330 mV, respectively. Consequently, as illustrated in Figure 3, most of the cations that pass through mechanically-activated PIEZO channels are likely to be Na+ and Ca2+, but not K+ (because of its small and negative ion motive force of –33 mV).
The mechanically-activated inward ionic currents in a range from a few pA to 100s pA per cell were measured [9] as a function of mechanical “touch” pressure as shown in Figure 4. A single PIEZO channel conductance was determined to be 22.9 ± 1.4 pS, which at a membrane potential of –70 mV can give rise to a mechanically-activated inward cation conduction rate of about 2 pA as shown in Figure 4C and D.
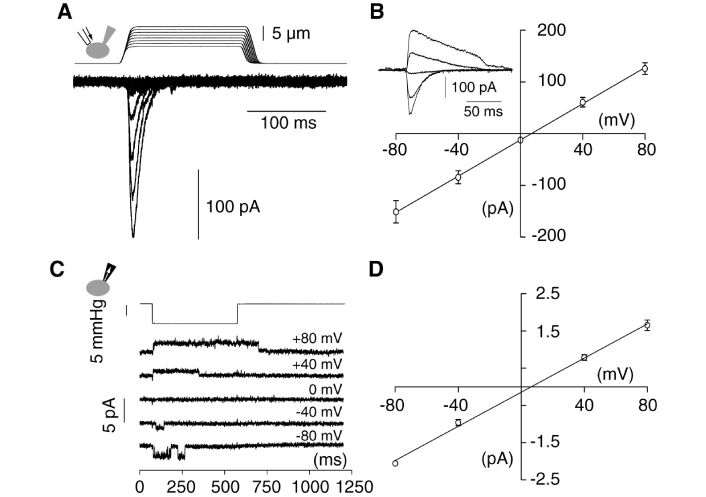
Mechanically-activated (MA) currents in Neuro2A (N2A) cells. (A) Representative traces of MA inward currents expressed in N2A cells. Cells were subjected to a series of mechanical steps of 1 μm movements of a stimulation pipette (inset drawing, arrow) in the whole-cell patch configuration at a holding potential of –80 mV; (B) average current-voltage relationships of MA currents in N2A (n = 11) cells. Inset, representative MA currents evoked at holding potentials ranging from –80 mV to +40 mV (applied 0.7 sec prior to the mechanical step); (C) single-channel currents (cell attached patch configuration) induced by negative pressure with a pipette (inset drawing, arrow) at holding potentials ranging from –80 mV to +80 mV in an N2A cell; (D) average current-voltage relationships of stretch-activated single channels in N2A cells [n = 4, mean ± standard error of the mean (SEM)]. Single channel conductance was calculated from the slope of the linear regression line of each cell giving γ = 22.9 ± 1.4 pS (mean ± SEM). Single channel amplitude was determined as the amplitude difference in Gaussian fits of full trace histograms
Note. Reprinted with permission from “Piezo1 and Piezo2 Are Essential Components of Distinct Mechanically Activated Cation Channels” by Coste B, Mathur J, Schmidt M, Earley TJ, Ranade S, Petrus MJ, et al. Science. 2010;330:55–60 (https://doi.org/10.1126/science.1193270). © 2010, American Association for the Advancement of Science.
The experimental data (Figure 4A) show that the PIEZO cation conduction rates can be in a range from 0 pA to more than 200 pA per cell, apparently depending on how many PIEZO channels were mechanically activated when the N2A cells were subjected to a series of mechanical steps of 1 μm movements of a stimulation pipette in the whole-cell patch configuration at a holding potential of –80 mV in the experiments [9]. The mechanically activated PIEZO cation conduction rates are also dependent on the experimentally applied holding potentials (voltage) ranging from –80 mV to +80 mV (Figure 4B). With negative pressure pulses evoked opening of endogenous channels (Figure 4C), a single PIEZO-channel conductance was measured to be 22.9 ± 1.4 pS (Figure 4D) [9].
It is now known that the Piezo1 and Piezo2 genes encode mechanically activated cationic channels that function as mechanotransducers involved in many physiological functions [17]. The Piezo2 unitary conductance is 23.7 ± 0.6 pS, which is about the same as that of Piezo1 (22.9 ± 1.4 pS) [39]. In the numerical analysis here, the experimentally measured Piezo1 unitary conductance of 22.9 ± 1.4 pS will be used as a typical PIEZO-channel conductance in our calculation here so that its results may have generic implications on the primary process of PIEZO-associated neural stimulation in firing action potential spikes for many physiological functions including (but not limited to) both vascular system development regulation and touch sensing [40–45].
Using the experimentally measured single PIEZO-channel conductance of 22.9 ± 1.4 pS, our calculation (conductance × transmembrane potential) result showed that the peak cationic-conduction current per PIEZO channel is about 1 pA to 2 pA when the neural transmembrane potential is a range from –40 mV to –90 mV, which is in line with the experimental results (Figure 4C and D). At the resting neural transmembrane potential of –70 mV, the peak cationic-conduction current per PIEZO channel was calculated to be 1.6 pA.
As mentioned previously, it is now known that for a neural transmembrane potential to change from the resting potential (–70 mV) to the stimulation threshold level (–55 mV) would require a threshold change of 800 TELC per μm2 from 3,900 to 3,100 TELC per μm2 on the extracellular membrane surface. Therefore, Equation 4 can be used to calculate either the PIEZO-channel cationic-conduction rate (I) or the time (t) required to produce a change of 800 TELC per μm2 for a neural cell to induce the firing of an action potential spike.
The experimental data (Figure 4) showed that the PIEZO cationic conduction rates can be in a range from about 0 pA to more than 200 pA per cell, apparently depending on how many PIEZO channels are mechanically activated by a particular touch. Therefore, to better understand TELC modulation with PIEZO by touch for neural stimulation, we calculated the TELC density change per μm2 of extracellular membrane surface as a function of time with a series of PIEZO cationic conduction rates (0.5 pA, 1 pA, 2 pA, 5 pA, 10 pA, 30 pA, 50 pA, 100 pA, 200 pA, 300 pA, and 500 pA) for a typical N2A cell that has a volume of about 2,700 μm3 and a total extracellular membrane surface area of 1,000 μm2. Figure 5 presents the TELC density changes calculated as a function of time with each of the given PIEZO cationic conduction rates in comparison with the threshold change of 800 TELC per μm2 (the dot line level in Figure 5) that is needed to reduce the TELC density from the resting level of 3,900 TELC per μm2 (equivalent to the resting potential of –70 mV) to the neural stimulation level of 3,100 TELC per μm2 (equivalent to the transmembrane potential of –55 mV) to trigger an action potential firing in a typical N2A cell.
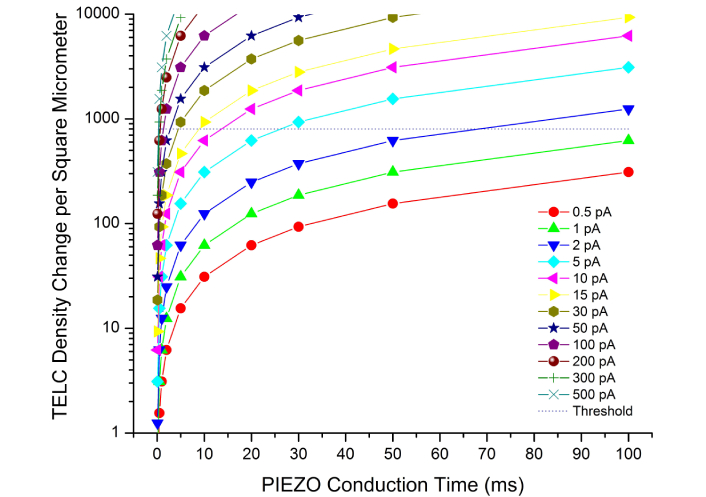
Touch signal transduction responding time. Modulation of transmembrane-electrostatically localized protons/cations charges (TELC) density change as a function of PIEZO channel cationic conduction time with various PIEZO cationic conduction rates in a range from 0.5 pA to 500 pA per Neuro2A (N2A) cell
As shown in Figure 5, the use of PIEZO channel cation conduction at its rate of 1–2 pA would need about 100 ms to produce the needed change of 800 TELC per μm2 (the dot line level in Figure 5) to reduce the TELC density from the resting level of 3,900 TELC per μm2 (at the rest potential of –70 mV) to the neural stimulation level of 3,100 TELC per μm2 (at the stimulation membrane potential of –55 mV), which can trigger an action potential firing. This result indicates that it may be possible for the use of a single PIEZO channel activity at its cationic-conduction rate of 2 pA for about 64 ms in a typical N2A cell with 1,000 μm2 of extracellular membrane surface area to induce an action potential firing.
Note, Piezo1 and Piezo2 channels typically display inactivation properties that are voltage dependent [40, 46, 47]. This could mean that a single PIEZO channel might not be able to stay open for 64 ms. In that case, more than a single PIEZO channel activity may be required to result in an action potential firing. On the other hand, N2A cells are model neuronal cells where PIEZO channel activity was first experimentally demonstrated. However, they are not truly mechanosensory receptor cells. Touch detection occurs in the nerve terminals of dorsal root ganglia (DRG) neurons that are bipolar neuronal cells projecting to the skin [48, 49]. It means that at sites of signal initiation by Piezo channels regarding touch, the size of neuronal compartment is smaller than the whole cell body. Consequently, it may still be possible for the activity of a single or a few PIEZO channels upon touch to induce an action potential firing.
The touch response from the onset of PIEZO channel cationic conduction activities to reduce the TELC density to the stimulation level of 3,100 TELC per μm2 can be quicker when a higher number of PIEZO channels are activated by the touch. For example, when five PIEZO channels are activated by touch, it can have the PIEZO channel cationic conduction rate as high as 10 pA. With the use of 10 pA of PIEZO channel cationic conduction in an N2A cell, it will need a calculated neural touch signal transduction responding time of about 13 ms to produce a TELC change as a “graded potential” from the resting potential (–70 mV) to the stimulation threshold level (–55 mV) by its corresponding change (reduction) of 800 TELC per μm2 (the dot line level in Figure 5) from 3,900 to 3,100 TELC per μm2 on the extracellular membrane surface to trigger an action potential firing.
As shown in the data (Figure 5) calculated through Equation 5, for an N2A cell with touch-actived PIEZO channel cation conduction rate at 15 pA, 30 pA, 100 pA, 200 pA, or 500 pA, it will need a calculated neural touch signal transduction responding time of about 8.5 ms, 4.3 ms, 1.3 ms, 0.6 ms, or 0.3 ms, respectively, to reach the needed change of 800 TELC per μm2 (the dot line level in Figure 5) from 3,900 to 3,100 TELC per μm2 to trigger a firing of an action potential spike in an N2A cell with 1,000 μm2 of extracellular membrane surface area.
Notably, based on the data (Figure 5) as calculated through Equation 5, the tough signal transduction responding time needed to produce a needed change of 800 TELC per μm2 from the resting potential level (–70 mV, 3,900 per μm2) to the stimulation level (–55 mV, 3,100 TELC per μm2) can be as short as 0.3 ms in a neural cell like a typical N2A cell with touch-activated PIEZO cation conduction rate of 500 pA. That is, when a high number of PIEZO channels are activated by touch, it can quickly induce an action potential firing within about 0.3 ms of tough signal transduction responding time.
The numbers of TELC per μm2 and per cell on the neuronal extracellular membrane surface were calculated from the total TELP/cations concentration
Figure 6 presents a comparison of a typical neural action potential “spike” with the corresponding curve of TELC per μm2 on the neuronal extracellular membrane surface in a real time domain of an action potential spike as calculated using Equations 1–5. The TELC curve has an inverse relationship with the action potential since its curve appears as an inverse mirror image of the action potential spike.
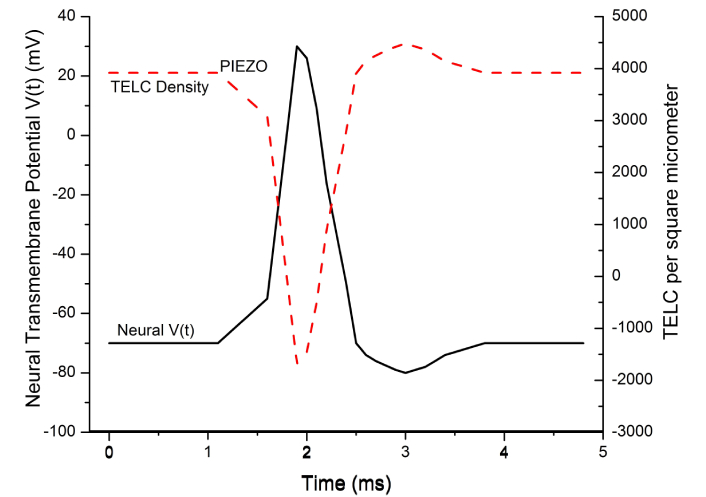
The inverse relationship between transmembrane-electrostatically localized protons/cations charges (TELC) and transmembrane potential. The inverse relationship between TELC density (charges per μm2) and action potential (mV) shown as the real-time TELC density is changed from its resting potential level (–70 mV, 3,900 TELC/μm2) at the time 1.1 ms through the touch-activated PIEZO channel cation conduction activity [IPIEZO(t)] to the stimulation level (–55 mV, 3,100 TELC/μm2) by the time at 1.6 ms, which triggers a firing of an action potential spike. The time-dependent TELC density (TELC per μm2) was calculated using Equation 5 and the action potential spike was calculated using Equation 7
In the example of time-dependent TELC and membrane potential with PIEZO as shown in Figure 6, the initial TELC surface density at time t = 0, TELC0, was 3,900 (protons + cations) per μm2 at its corresponding rest potential level (–70 mV). During the period from 0 to 1.1 ms at the resting state, the net transmembrane channel cationic (and anionic) conduction current I(t) was zero so that its integral as the first term of Equation 5 was zero and thus the TELCt remained as a flat curve at the TELC0 level of 3,900 (protons + cations) per μm2. Correspondingly, the transmembrane potential Vt remained as a flat curve at the V0 level of –70 mV.
During the “graded potential” period from 1.1 ms to 1.6 ms, the transmembrane channel ionic conduction current I(t) was a PIEZO-enabled cation current [IPIEZO(t)] of about –0.25 pA/μm2 (–250 pA per cell or –1.6 × 106 charges/s•μm2) owning to the “touch” mechanically-activated PIEZO channel cationic conduction current “flows into the cell” as illustrated in Figure 3. The integration of I(t) with dt (the first term of Equation 5) for the period from 1.1 ms to 1.6 ms yielded a TELC density change of –800 (protons + cations) per μm2 that thus reduced the TELCt level from the resting level of 3,900 to the stimulation level of 3,100 per μm2 as shown in Figure 6. Correspondingly, in accordance with Equations 6 and 7, the transmembrane potential Vt curve as a “graded potential” rose from the resting level of –70 mV to the simulation level of –55 mV, which is known to trigger an opening of voltage-gated sodium channels, resulting in an action potential firing (Figure 6).
During the “action potential firing depolarization” period from 1.6 ms to 1.9 ms for the rising phase of an action potential spike, the transmembrane channel ion conduction current I(t) was the INa(t) of –2.5 pA/μm2 from the opening of voltage-gated sodium channels that resulted in a substantial sodium (cation charge) conduction of –1.6 × 107 charges/s•μm2 from the extracellular side to the intracellular side as illustrated in Figure 2A. Consequently, its integral as the first term of Equation 5 (for the TELC density change during the period from 1.6 ms to 1.9 ms) was calculated to be a large negative number (–4,800 charges/μm2) while the corresponding Vt integral of Equation 6 (for the transmembrane potential change) yielded a substantial positive number of +85 mV. This mathematically explained the inverse relationship between the TELCt curve and the Vt curve at the rising phase of the action potential spike as shown in Figure 6, which showed a dramatic decline (corresponding to “depolarization”) in the TELC density to a negative number well below zero (–1,700, corresponding to the action potential of about +30 mV at the time of 1.9 ms) where the voltage-gated sodium channels would shut and the voltage-gated potassium channels would open.
During the “repolarization” period after the time of 1.9 ms for the falling phase of the action potential spike, the transmembrane channel ion conduction current I(t) was the IK(t) of about +1.5 pA/μm2 from the opening of the voltage-gated potassium channels that allowed the K+ cations flowing (9.4 × 106 K+/s•μm2) out of the cell “from the intracellular site to the extracellular side” as shown in Figure 2B. Consequently, its integral as the first term of Equation 5 (for TELC density change) for the time from 1.9 ms to 2.5 ms was calculated to be a large positive number of 5,600 charges/μm2; while the corresponding Vt integral of Equation 6 resulted in a large negative number of –100 mV for the transmembrane potential change so that the time-dependent transmembrane potential Vt returned from the peak level of +30 mV (at 1.9 ms) to a resting level of –70 mV at the time of 2.5 ms. This mathematically also explained the inverse image between the TELCt curve and the Vt curve at the falling phase of the action potential spike during the repolarization as shown in Figure 6, which manifested a rapid rise of TELC density from the negative number (–1,700 at 1.9 ms) back to a positive number of 3,900 charges/μm2 at the time of 2.5 ms.
As shown in Figure 6, the repolarization was then followed by an “undershoot” (to about –80 mV with TELC density reaching as much as +4,500 charges per μm2) at the time of 3.0 ms and subsequently re-equilibrating with the activities of the “leaky channels” of other ions likely including chloride channels and ATP-driven sodium/potassium (Na+/K+) pumps (Figure 1B) back to –70 mV (+3,900 charges per μm2) at the time of 3.8 ms. Thereafter, since the net transmembrane channel ion conduction current I(t) remained zero, it resulted in the flat Vt curves from 3.8 ms to 4.8 ms for the re-established resting state in this example. This explained the time-dependent TELC and transmembrane potential with the integral equations (Equations 5, 6, and 7) for a PIEZO-induced action potential spike from its beginning to its end.
ATP: adenosine triphosphate
N2A: Neuro2A
TELC: transmembrane-electrostatically localized protons/cations charges
TELCt: time-dependent transmembrane-electrostatically localized charge density
TELP: transmembrane-electrostatically localized protons
The supplementary material for this article is available at: https://www.explorationpub.com/uploads/Article/file/100685_sup_1.xlsx.
Special thanks to Dr. Bertrand Coste (CNRS, France) for his highly insightful review and suggestion feedbacks on this manuscript.
JWL: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Software, Resources, Supervision, Validation, Visualization, Writing—original draft, Writing—review & editing.
The author declares no conflicts of interest.
Not applicable.
Not applicable.
Not applicable.
All datasets generated for this study are included in the manuscript and the supplementary files.
This research was supported in part by a Multidisciplinary Biomedical Research Seed Funding Grant from the Graduate School, the College of Sciences, and the Center for Bioelectrics at Old Dominion University, Norfolk, Virginia, USA. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
© The Author(s) 2025.
Open Exploration maintains a neutral stance on jurisdictional claims in published institutional affiliations and maps. All opinions expressed in this article are the personal views of the author(s) and do not represent the stance of the editorial team or the publisher.
Copyright: © The Author(s) 2025. This is an Open Access article licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, sharing, adaptation, distribution and reproduction in any medium or format, for any purpose, even commercially, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
