Abstract
Aim:
Since its emergence in 2019, coronavirus disease 2019 (COVID-19) has evolved into a global pandemic, placing extraordinary strain on healthcare systems and societies worldwide. Accurate forecasting of COVID-19 case trends is essential for effective public health planning and intervention.
Methods:
This study employs the Susceptible-Infectious-Recovered (SIR) model to predict the progression of COVID-19 in three countries: Belarus, Thailand, and Lithuania. Instead of relying on static or globally derived estimates, the model parameters—infection rate (β) and removal rate (γ)—were dynamically calculated for distinct time periods in each country, using country-specific data extracted from Worldometer. This segmented approach accounts for temporal changes in transmission dynamics and public health responses.
Results:
The country-specific, phase-based parameter estimation improved the model’s alignment with real-world COVID-19 trends observed in Belarus, Thailand, and Lithuania. The refined forecasts closely matched the actual progression patterns in each country, demonstrating the value of adapting parameter estimates to local epidemiological contexts.
Conclusions:
The proposed approach enhances the predictive accuracy of the SIR model, providing a practical and adaptable framework for forecasting COVID-19 trends in countries with varying pandemic responses. These findings highlight the importance of dynamic parameter adjustment when applying mathematical models to evolving public health crises, ensuring more reliable projections to guide decision-making.
Keywords
COVID-19, Susceptible-Infectious-Recovered (SIR) simulation, disease prevalence, epidemiological forecasting, temporal phasesIntroduction
In December 2019, a novel coronavirus, later identified as severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), emerged, marking the beginning of an unprecedented global health crisis [1]. Within months, this highly transmissible virus triggered a global pandemic, spreading across continents and severely impacting public health systems, economies, and social structures [2, 3]. COVID-19, the disease caused by SARS-CoV-2, presents a wide spectrum of symptoms, ranging from mild respiratory issues to severe pneumonia, with fever, cough, and anosmia among the most common clinical manifestations [2].
Efforts to mitigate the spread of the virus have involved public health interventions such as mask mandates, social distancing, quarantine measures, and widespread disinfection protocols [4]. Some countries adopted extensive lockdowns to break transmission chains, though these measures were challenged by the virus’s asymptomatic carriers, insufficient healthcare infrastructure in certain regions, and the complexities of implementing population-wide interventions [5].
Mathematical modeling has played a critical role in understanding the spread and control of infectious diseases. Epidemiologists frequently rely on compartmental models to simulate disease dynamics and assess the potential impact of preventive strategies such as quarantine and social distancing [2]. Among these models, the Susceptible-Infectious-Recovered (SIR) framework remains one of the most fundamental and widely used approaches for predicting the trajectory of epidemics [6].
A range of studies has employed various modeling techniques to predict the progression of COVID-19 and guide policymakers in decision-making. For example, some research has focused on the psychological effects of the pandemic, using methods such as Pearson correlation and multiple regression to explore the link between coronavirus-related anxiety and students’ learning anxiety [7]. Other studies have employed machine learning techniques, such as decision trees, to compare disease progression across different countries [8], while Long Short-Term Memory (LSTM) networks have been used to forecast case numbers in countries like India, Brazil, and the United States [9]. Additionally, models originally developed for SARS have been adapted to predict COVID-19 trends, particularly in Iran [10], and the Susceptible-Exposed-Infectious-Recovered (SEIR) model has been utilized to analyze disease dynamics in the same region [11]. Several studies have also applied graphical analyses to identify key indicators for effective pandemic management [12], and system dynamics modeling has been used to examine disease progression across various provinces in Iran [13].
While these studies have significantly advanced the understanding of COVID-19 dynamics, they have largely focused on short-term predictions or specific geographical contexts. There remains a critical need for comprehensive, data-driven modeling to assess long-term transmission patterns and guide public health responses in diverse settings. This study addresses that gap by analyzing the spread of COVID-19 in Lithuania, Belarus, and Thailand using the SIR model. Data obtained from Worldometer, a widely used platform for global COVID-19 statistics, were employed to update the model parameters and simulate disease progression in these three countries.
The following sections of this paper review previous research on COVID-19 prediction, describe the SIR model and its application, present the results of modeling COVID-19 dynamics in Lithuania, Belarus, and Thailand, and conclude with key findings and their implications for future pandemic preparedness.
Previous works
Considering the significant impact of COVID-19 prediction modeling in assisting countries with control decisions and preventing the spread of the disease, it’s clear that this field holds paramount importance. Numerous research studies have been conducted globally, including in Iran, to explore various prediction methods.
COVID-19 presents a wide clinical spectrum, from asymptomatic cases to severe respiratory failure, with older adults and those with pre-existing conditions facing the highest risks [14, 15]. Routine hematologic markers, including neutrophil-to-lymphocyte ratio (NLR) and platelet-to-lymphocyte ratio (PLR), have shown strong associations with disease severity and prognosis [16–18]. Red cell distribution width (RDW) and inflammatory indices like mean platelet volume (MPV) and monocyte-to-lymphocyte ratio (MLR) further aid in risk stratification, especially in high-risk populations such as diabetics [19, 20]. These accessible markers offer valuable tools for early assessment and long-term monitoring in COVID-19 management.
One study by Shomaliahmadabadi et al. (2021) [7] examined the role of coronavirus-related anxiety and negative metacognitive beliefs in predicting students’ learning anxiety. This descriptive research used an expanded correlation method and surveyed the entire population of female middle school students in Isfahan, Iran, during the 1399–1400 academic year (Iranian calendar, equivalent to 2020–2022 in the Gregorian calendar). The findings suggest that COVID-19 concerns and negative metacognitive beliefs can lead to increased learning anxiety. The researchers recommend implementing educational programs through various media channels, particularly radio and television, to modify students’ beliefs and reduce their anxiety, ultimately leading to improved academic performance.
Another study by Boskabadi and Doostparast (2020) [8] employed decision tree methods or regression to compare and predict the disease’s progression in countries like China, France, Germany, Iran, and others. Decision trees are non-parametric classification techniques widely used in data mining. They can be categorized as tree classification for discrete variables or tree regression for continuous variables. These methods, also known as CART (Classification and Regression Trees), can model and analyze both classification and regression scenarios.
The results obtained from this modeling reflect the impact of societal control on disease progression and the influence of this method in managing the reduction of screening costs and quarantines. Kadivar and Keshavarz Mohammadi (2020) [9] conducted a study using the LSTM method to predict the number of COVID-19 patients in three countries: India, Brazil, and the United States, which have the highest number of COVID-19 cases. LSTM, an improved form of the Recurrent Neural Network (RNN), has strong capabilities in predicting time series data. As a neural network, LSTM receives a set of samples as input and predicts the number of patients in future days based on configured settings. Moreover, the results obtained from this modeling indicate the level of prediction error, directly reflecting the accuracy of the modeling.
Hoseinpour Dehkordi et al. (2020) [10] conducted a modeling simulation through the Corona Team of Liujen Farmed Company, utilizing the SARS epidemic model to predict COVID-19 cases in Iran. Their study found a remarkable similarity between the epidemiological patterns of SARS and COVID-19, highlighting the potential applicability of the SARS model for predicting COVID-19 cases. However, the model demonstrated certain limitations, particularly in short-term predictions.
Ghaffarzadegan and Rahmandad (2020) [11] developed a dynamic and straightforward epidemic model in Iran, based on the SEIR framework. This model incorporates behavioral and logistical observations, particularly changes in contact rates and the mechanisms driving disease progression, providing a more reliable representation of the pandemic’s status based on available data.
Abbasimehr and Paki (2020) [12] examined key indicators related to the spread of COVID-19 and their practical applications in enhancing the understanding and management of the pandemic. Their study applied graphical analysis to historical data from countries such as Germany, Iran, and South Korea. The goal was to provide a comprehensive and critical assessment of essential indicators, explore their practical applications in pandemic management, and offer recommendations for optimal monitoring indicators to evaluate healthcare system performance. Their modeling covered a 14-day forecasting period, which is relatively short compared to other approaches.
In another modeling study, Salehi Va Shafiei and Makari Ghahroudi (2020) [13] investigated the prediction of COVID-19 progression using system dynamics modeling across various provinces of Iran.
Moreover, Kraemer et al. (2020) [21] examined how human mobility patterns and timely control measures significantly influenced the trajectory of COVID-19 in China, providing valuable insights into the relationship between movement restrictions and infection rates.
Extensive research has been conducted to better understand the evolution, transmission, and treatment strategies for SARS-CoV-2. Araf et al. [22] highlighted the Omicron variant’s high transmissibility, increased risk of reinfection, and uncertainties regarding vaccine effectiveness. Zhang et al. [23] reviewed global efforts in vaccine and antiviral development, comparing SARS-CoV-2 with related coronaviruses. Farheen et al. [24] examined the emergence of the recombinant “Deltacron” variant, emphasizing the importance of closely monitoring its epidemiological characteristics. Chakraborty et al. [25] applied structural biology methods to investigate the interaction between SARS-CoV-2’s main protease (Mpro) and the antiviral drug nirmatrelvir, providing valuable insights for future antiviral drug design. Cui et al. [26] underscored the ongoing threat posed by zoonotic transmission of SARS-CoV-2 between humans and animals, highlighting the importance of cross-species surveillance. Zhai et al. [27] explored the zoonotic potential of porcine deltacoronavirus, stressing the need for monitoring coronaviruses in animal populations. Prapty et al. [28] addressed the challenges of diagnosing and treating co-infections of SARS-CoV-2 and dengue virus, particularly in dengue-endemic regions, emphasizing the importance of dual diagnostic protocols.
The purpose of this article is to address the existing gaps in previous studies, notably the long-term impacts of COVID-19 changes. Nearly all models have assumed that recovered individuals will not be reinfected with the disease. This study challenges this assumption based on recent reports. A new discovery by laboratory researchers shows the virus’s strength, indicating a potential threefold increase in the transmission rate. In this research, three models with different variables are considered, compared, and conclusions are drawn from these models. The findings highlight the comparison of disease engagement levels in various areas of Iran and the examination of the impact of travel restrictions and containment measures.
The predictions so far have been conducted in various countries, including Iran, China, France, Brazil, the United States, Italy, Japan, Spain, Germany, and South Korea, among many others. However, these predictions have some weaknesses:
Most of these articles are written using a comparative approach, and their primary focus is not on predicting the trends of the disease in their respective countries.
Some articles have made short-term predictions.
In the LSTM prediction model, due to its complexity and extensive computational processes, there is a significant potential for measurement errors.
To the best of our knowledge, there is a lack of comprehensive modeling studies specifically focusing on the prediction of COVID-19 progression in the three countries of Lithuania, Belarus, and Thailand.
Thus, in this paper, statistical data from these three countries—Lithuania, Belarus, and Thailand—have been processed using the SIR model, a mathematical computational model whose functionality has been proven. The article emphasizes long-term predictive results.
Materials and methods
This study uses a mathematical modeling approach to simulate the spread of COVID-19 in Lithuania, Belarus, and Thailand. The classical SIR model was applied to predict the progression of the disease in these countries. To ensure the accuracy and applicability of the model, real-time case data were used to estimate key parameters over distinct phases of the pandemic in each country. This section outlines the data sources, selection criteria, modeling framework, segmentation approach, software tools, and methodological considerations that collectively ensure transparency, reproducibility, and alignment with evolving pandemic dynamics.
Data source and inclusion criteria
Daily confirmed COVID-19 case data for Lithuania, Belarus, and Thailand were obtained from Worldometer (https://www.worldometers.info/coronavirus/), accessed on September 30, 2021. This publicly available platform aggregates official case data from national health authorities, offering consistent and comparable data across countries. Moreover, the selection of Lithuania, Belarus, and Thailand was based on the availability of reliable, continuous case data, as well as the diversity in their pandemic response strategies, healthcare infrastructure, and population densities. These countries represent three distinct pandemic contexts, allowing the SIR model to be tested across varying epidemiological environments, thereby enhancing the robustness of the analysis.
In addition, all simulations and parameter estimations were conducted using MATLAB version R2021a (MathWorks, Inc., Natick, Massachusetts, USA). Curve fitting procedures were performed using MATLAB’s built-in Nonlinear Least Squares (lsqcurvefit) function, and visualizations were generated using MATLAB plotting tools.
SIR model
The SIR model is a fundamental mathematical tool used to analyze the spread of infectious diseases within a population [22]. It simplifies the population into three compartments: Susceptible (S), Infectious (I), and Recovered (R). Equation 1 represents this model mathematically:
Susceptible (S): This group consists of healthy individuals who haven’t contracted the disease yet but can become infected [2].
Infectious (I): This category represents individuals who are currently infected and can transmit the disease to others [2].
Recovered (R): This group includes individuals who have recovered from the disease and are no longer infectious [2]. It’s important to note that for some diseases, recovered individuals may become susceptible again (e.g., the common cold).
These variables (S, I, and R) change dynamically as the disease progresses. The rate of infection is denoted by “r”, which represents the constant rate at which susceptible individuals come into contact with infected individuals and become infected themselves [29]. The other parameter, denoted by the Greek letter beta (β), represents the constant rate at which infected individuals are removed from the infectious pool, typically due to recovery or, unfortunately, mortality [29].
The SIR model’s compartmentalization of disease states (Figure 1A) and its application to COVID-19 for analyzing and predicting disease spread, informing public health decisions, and implementing control measures (Figure 1B). While the top portion of Figure 1 illustrates a standard SIR model, the bottom portion adapts it for COVID-19 by accounting for the possibility of recovered individuals becoming susceptible again, a concept crucial for understanding COVID-19 transmission.
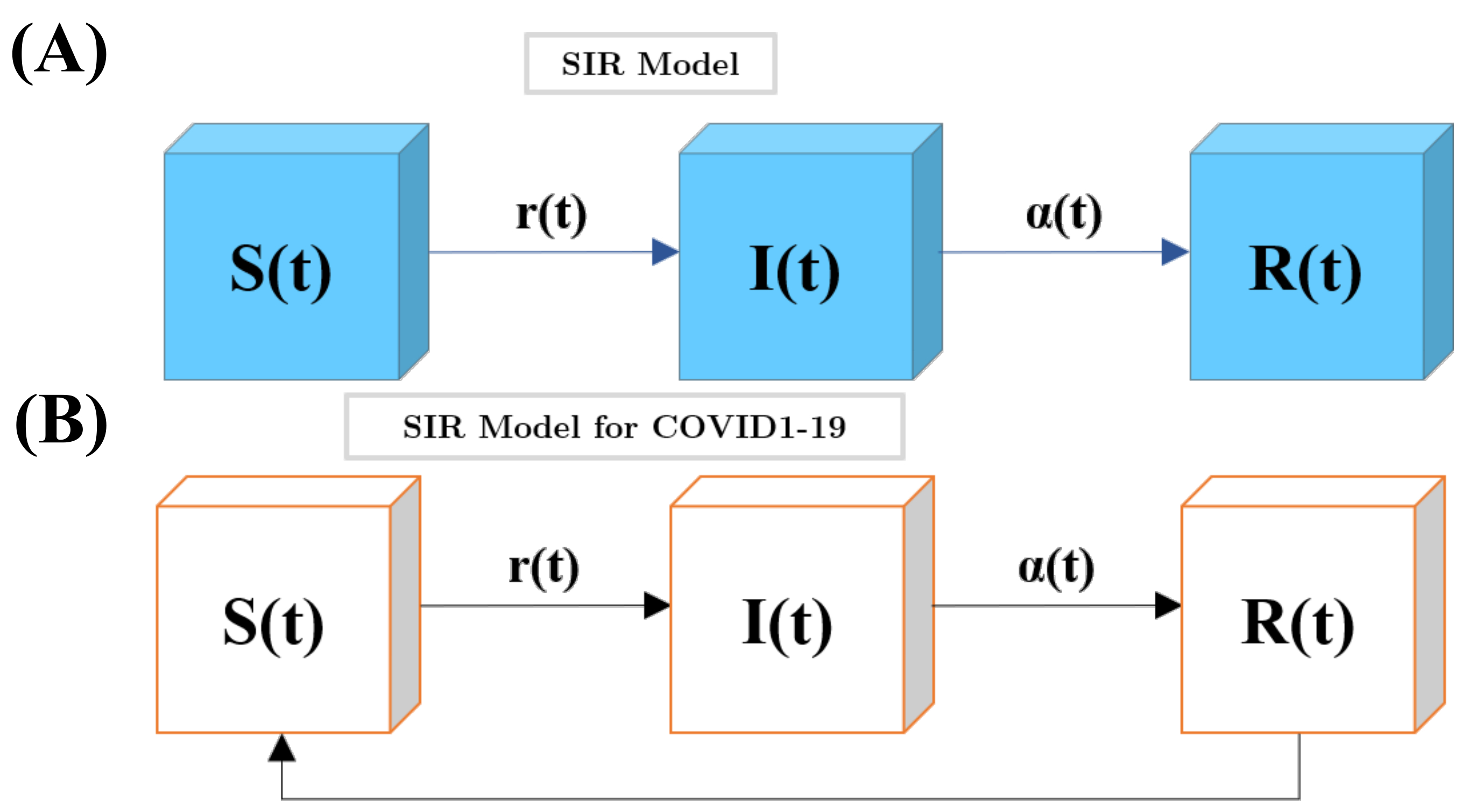
The SIR model’s structure and applications. (A) Compartmentalization of disease states; (B) application to COVID-19 for analyzing and predicting disease spread, informing public health decisions, and implementing control measures
The total number of people is defined as N, which is the sum of three groups [30], as shown in Equation 2.
Prevalence and transmission rates are also shown in Equation 3.
Where R0 indicates whether a disease is rapidly subsiding or causing an epidemic in the community [21, 31].
Time segmentation
To account for changes in transmission dynamics over the course of the pandemic, the data for each country were divided into distinct phases based on observed inflection points in case trends, which often corresponded to major policy changes such as lockdowns, reopening phases, or mass vaccination campaigns. Each phase was modeled separately, with β and γ recalculated for each period, ensuring the model remained responsive to evolving real-world conditions.
Uncertainty analysis
This study primarily relied on fitting the SIR model to reported COVID-19 case data using a deterministic curve-fitting approach, where key parameters—the infection rate (β) and removal rate (γ)—were estimated directly from observed data during distinct time periods. While this method provides a practical way to align the model with real-world data, it does not explicitly quantify the uncertainty associated with these parameter estimates. In particular, factors such as underreported infections, variations in testing capacity, changes in public health interventions, and differences in population behavior can introduce unavoidable uncertainties into both parameter estimation and model projections. These sources of variability were not formally analyzed in the current study, representing a recognized limitation of the approach. The focus of this research was to evaluate the applicability of the classical SIR model in capturing the overall epidemic trends across three countries with varying pandemic responses.
Methods of using the model for data
The model was implemented using MATLAB software, employing mathematical functions such as fminsearch and lambertw to test the code. In cases where the predicted results from Equation 4 do not align, the equation seeks an appropriate solution within the range of [–1e6, 1e6] for forecasting purposes.
The simulation data for three countries—Lithuania, Belarus, and Thailand—were obtained from the Worldmeter website and analyzed. Ultimately, three model graphs were generated, depicting the parameter values on each graph. These values include R, which denotes the primary (total) rate, and R0, which indicates the infection rate predicting the disease’s growth. If R0 < 1, it means the number of patients is decreasing, and the disease is declining. However, if R0 > 1, it signifies an increasing trend in the spread of the disease. Other parameters include:
β indicates the infection rate, measuring the daily increase in patients.
γ represents the removal rate, measuring the daily count of removed patients, including recovered or deceased individuals.
N represents the population of the respective country.
Cend indicates the final number of infected individuals.
Send represents the difference between the final number of infected individuals and the population of the respective country.
Root mean square error (RMSE) signifies the Root Mean Square Error in regression.
Data used in this study were collected from the Worldometer website, which provides real-time global COVID-19 data (Available at: https://www.worldometers.info/coronavirus/, accessed on 30 September 2021). The simulation and modeling processes were conducted using MATLAB version R2021a (MathWorks, Inc., Natick, Massachusetts, USA).
Results
Numerical simulation
In this section, the results of modeling for Lithuania, Belarus, and Thailand are investigated.
Lithuania
The estimation of this disease model has been compared using real data from Lithuania from March 14, 2020, to September 30, 2021. As shown in Table 1 and Figure 2, R0, indicating the rate of disease spread, initially rises until February, followed by a declining trend.
Statistical analysis of Lithuania
| Date | R | R0 | β | γ | N | Cend | Send | RMSE |
|---|---|---|---|---|---|---|---|---|
| Mar, Apr 2020 | 0.52 | 1.56 | 0.391 | 0.25 | 2,375 | 1,501 | 874 | 61 |
| May, Jun 2020 | 0.18 | 3 | 0.196 | 0.065 | 1,750 | 1,601 | 149 | 106 |
| Jul, Aug 2020 | 0.14 | 3.31 | 0.19 | 0.058 | 2,041 | 1,956 | 85 | 290 |
| Sep, Oct 2020 | 3.94 | 4.11 | 0.106 | 0.06 | 262,221 | 257,592 | 4,629 | 2,222 |
| Nov, Dec 2020 | 0.95 | 1.48 | 0.167 | 0.113 | 403,045 | 229,730 | 173,315 | 1,693 |
| Jan, Feb 2021 | 0.64 | 46.19 | 0.059 | 0.001 | 197,727 | 197,727 | 0 | 2,181 |
| Mar, Apr 2021 | 0.24 | 2.89 | 0.077 | 0.027 | 241,947 | 225,512 | 16,435 | 5,486 |
| May, Jun 2021 | 0.45 | 1.89 | 0.114 | 0.06 | 285,025 | 218,140 | 66,885 | 20,169 |
| Jul, Aug 2021 | 0.38 | 2.07 | 0.103 | 0.05 | 272,252 | 221,929 | 50,323 | 28,112 |
| Sep 2021 | 0.3 | 2.49 | 0.044 | 0.018 | 330,765 | 294,672 | 36,093 | 13,583 |
RMSE: root mean square error
This decline is significantly attributed to vaccination efforts after that date, which have substantially reduced the rate of disease spread. Additionally, β is decreasing, signifying a lower infection rate. The highest removal rate is observed in March and April. Considering that the contact rate was high in these months and the previous month, it can be hypothesized that this high removal rate is a consequence of an increased number of fatalities during that period.
Belarus
To compare the model estimates for this disease, data from the actual situation in Belarus, from March 5, 2020, to September 30, 2021, were utilized. According to Table 2 and Figure 3, R0, which indicates the disease’s transmission rate, was significantly increasing until November 2020, suggesting a considerable increase in disease progression. After a two-month decline, it returned to its ascending trend. Following that, there has been a relatively descending trend.
Statistical data analysis of Belarus
| Date | R | R0 | β | γ | N | Cend | Send | RMSE |
|---|---|---|---|---|---|---|---|---|
| Mar, Apr 2020 | 0.99 | 1.61 | 0.412 | 0.256 | 33,071 | 21,476 | 11,595 | 213 |
| May, Jun 2020 | 0.61 | 1.81 | 0.163 | 0.09 | 91,312 | 67,370 | 23,942 | 1,046 |
| Jul, Aug 2020 | 0.33 | 2.33 | 0.121 | 0.052 | 81,451 | 70,675 | 10,776 | 959 |
| Sep, Oct 2020 | 0.16 | 3.17 | 0.145 | 0.046 | 78,177 | 74,360 | 3,817 | 6,693 |
| Nov, Dec 2020 | 2.13 | 2.58 | 0.013 | 0.005 | 960,801 | 869,242 | 91,559 | 13,048 |
| Jan, Feb 2021 | 0.86 | 1.28 | 0.129 | 0.101 | 703,069 | 285,667 | 417,402 | 52,817 |
| Mar, Apr 2021 | 0.65 | 2.27 | 0.037 | 0.016 | 439,475 | 376,379 | 63,096 | 41,727 |
| May, Jun 2021 | 0.91 | 1.13 | 0.123 | 0.109 | 445,956 | 19,976 | 425,980 | 26,217 |
| Jul, Aug 2021 | 0.65 | 1.76 | 0.03 | 0.017 | 718,322 | 517,572 | 200,750 | 21,119 |
| Sep 2021 | 0.93 | 1.1 | 0.097 | 0.088 | 3,248,480 | 590,778 | 2,657,700 | 14,715 |
RMSE: root mean square error
Importantly, the R0 values mostly fall within a narrow range, displaying little variation. This suggests the disease has mostly followed a consistent pattern with few notable fluctuations. Additionally, looking at β, the lowest infection rate occurred in November and December, while the infection rate was fairly consistent throughout the remaining months. Regarding γ, the highest removal rate was observed in March and April. This observation, considering the infection and disease progression rates in these months and the prior month, supports the hypothesis that the increase in the removal rate might be due to increased fatalities.
Thailand
For the comparison of the model estimation for this disease, actual data from Thailand spanning from March 25, 2020, to September 10, 2021, have been employed. According to Table 3 and Figure 4, the disease, after a steep ascent with a remarkably high slope, suddenly experienced a decline, showing fewer cases each day. This reflects the vaccination efforts of Thailand’s population. This country, renowned as a global tourist destination, enforced a nationwide quarantine, prohibiting the entry of foreign nationals, thus steering the disease into a downward trend. The disease’s rate of spread, R0, was considerably high up to November 2020, indicating an intense ascending trend with a steep incline, followed by a noticeable decline. With regard to the infection rate, β, it was notably lower in the last eight months than in the preceding months. Furthermore, the removal rate, 𝛾, exhibited its highest values in the months of March and April, signifying the most recoveries and removals. Considering the abrupt contraction of the disease rate and the vaccination campaigns after this date, it can be inferred that the increase in this rate was not due to fatalities but was rather the result of recoveries. One distinguishing feature in the graph of this country, in comparison to the other two countries, is the arc curvature of the graph, which neither Belarus nor Lithuania exhibits.
Statistical analysis of Thailand
| Date | R | R0 | β | γ | N | Cend | Send | RMSE |
|---|---|---|---|---|---|---|---|---|
| Mar, Apr 2020 | 0.51 | 1.5 | 0.294 | 0.196 | 58 | 40 | 18 | 2 |
| May, Jun 2020 | 0.15 | 4.52 | 0.251 | 0.055 | 2,975 | 2,940 | 35 | 53 |
| Jul, Aug 2020 | 0.15 | 3.2 | 0.258 | 0.081 | 3,235 | 3,081 | 154 | 56 |
| Sep, Oct 2020 | 0.15 | 3.2 | 0.167 | 0.052 | 3,409 | 3,248 | 161 | 121 |
| Nov, Dec 2020 | 0.18 | 3.01 | 0.292 | 0.097 | 3,151 | 2,965 | 186 | 348 |
| Jan, Feb 2021 | 0.42 | 1.97 | 0.212 | 0.108 | 4,592 | 3,618 | 974 | 551 |
| Mar, Apr 2021 | 0.79 | 1.48 | 0.173 | 0.117 | 49,165 | 27,884 | 21,281 | 2,900 |
| May, Jun 2021 | 2.2 | 2.21 | 0.025 | 0.011 | 898,976 | 760,951 | 138,025 | 2,977 |
| Jul, Aug 2021 | 1.03 | 1.48 | 0.106 | 0.071 | 847,056 | 482,523 | 364,533 | 6,503 |
| Sep 2021 | 0.94 | 1.5 | 0.126 | 0.084 | 3,431,830 | 1,997,320 | 1,434,510 | 35,022 |
RMSE: root mean square error
Progression of disease in the future
To calculate the disease trend, Tables 4 and 5 are used, which display the sum, mean, sample variance, and comprehensive variance.
Data and forecasting data from three countries
| Parameters | Lithuanian data forecast | Belarusian data forecast | Thai data forecast | Lithuanian data | Belarus data | Thai data |
|---|---|---|---|---|---|---|
| Sum | 289,553 | 509,498 | 1,299,964 | 306,611 | 503,697 | 1,353,422 |
| Average | 530.3168 | 918.0144 | 2,380.886 | 547.5196 | 899.4589 | 2,278.48822 |
| Sample variance | 314,359 | 161,824.3 | 28,259,246 | 567,080.5 | 491,405.7 | 27,260,180.9 |
| Community variance | 313,783.2 | 161,532.8 | 28,207,489 | 566,067.8 | 490,528.2 | 27,214,288 |
Error and absolute error of three countries
| Parameters | Lithuanian data forecast | Belarusian data forecast | Thai data forecast | Lithuanian data | Belarus data | Thai data |
|---|---|---|---|---|---|---|
| Sum | 188,896 | 216,631 | 291,904 | –17,058 | 5,801 | –53,458 |
| Average | 317.4723 | 364.857 | 490.595 | –28.6689 | 9.74958 | –89.8454 |
| Sample variance | 153,089.1 | 187,072.1 | 937,763.7 | 253,224.1 | 319,758.4 | 170,167 |
| Community variance | 152,831.8 | 186,757.7 | 36,187.6 | 252,798.6 | 319,221 | 1,168,799 |
By comparing the tables, we can see that the predictions are close to the actual values and that the prediction error is low. In Thailand, the disease reached its peak on August 21, 2021, and the number of cases has consistently declined since then. This decline can be attributed to vaccination efforts, adherence to health protocols, and the enforcement of quarantine measures. As shown in Figure 5A, the disease trend was consistently rising from the beginning of the outbreak until August 21, 2021, and has significantly declined afterward.
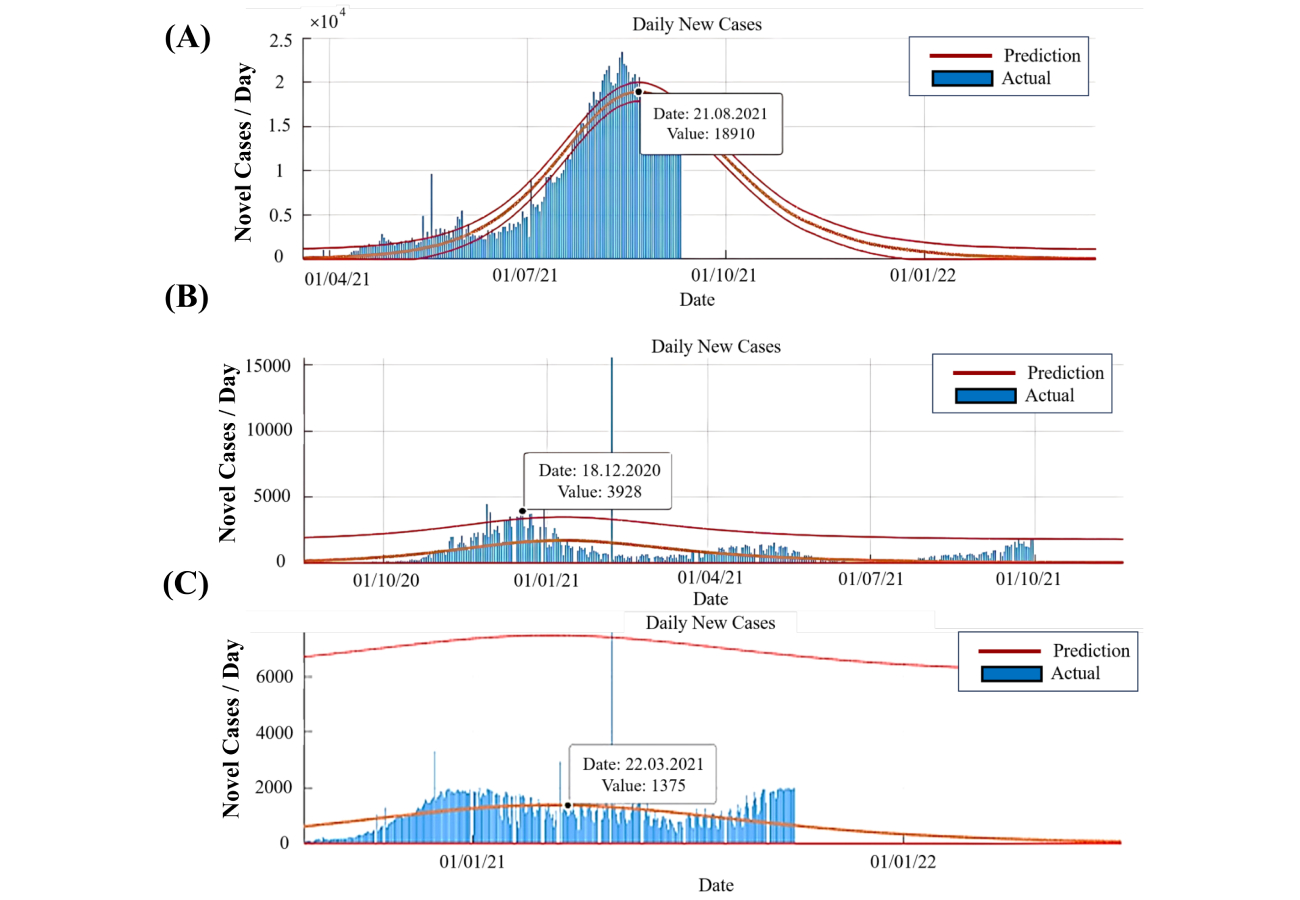
New daily patients. (A) In Thailand; (B) in Lithuania; (C) in Belarus. In Belarus, the trend shows a peak on March 22, 2021, followed by stability, mild fluctuations, and relatively stable daily patient numbers without significant changes
In Lithuania, the disease peaked on December 18, 2020. Following the initial peak, upward trends were observed on May 1, 2021, and September 23, 2021. However, the overall trend remains descending. Figure 5B shows a relatively consistent pattern, with no significant fluctuations in the trajectory. While there is a brief upward trend in the near future, the general trend is steadily declining compared to the peak.
In Belarus, the disease trend is predicted to follow a declining trajectory, with the peak occurring on March 22, 2021. The disease exhibited an upward trend until November 28, 2020, reached relative stability, followed by a mild downward trend from March 22, 2021, and a slight upward trend from August 5, 2021. As depicted in Figure 5C, the trend in Belarus lacks significant steep inclines or declines, with daily patient numbers remaining relatively stable.
Discussion
Implications for public health and policy
The findings from this study provide valuable insights into the progression and control of COVID-19, with direct implications for public health and policymaking. By leveraging the SIR model, decision-makers can gain a clearer understanding of infection dynamics, enabling more informed responses to the pandemic. This section discusses how the results can be applied to public health strategies and outlines actionable recommendations to mitigate the spread of the disease. The SIR model’s ability to forecast disease trends can aid governments in designing targeted vaccination campaigns. For instance, prioritizing high-transmission regions or groups based on model projections can significantly reduce infection rates. In Thailand, where the disease’s peak was mitigated by extensive vaccination efforts, the model underscores the importance of timely interventions. Policymakers can also use these projections to optimize resource allocation, ensuring vaccines reach areas predicted to experience rising cases.
The results highlight critical periods of disease escalation and decline, which can inform the timing and intensity of interventions such as lockdowns, travel restrictions, and public health campaigns. For example, in Belarus, the model identifies a stable period following an initial peak, providing an opportunity to reinforce preventive measures and avoid a resurgence. Similarly, the insights for Lithuania suggest that timely interventions during upward trends could have curtailed subsequent outbreaks. Beyond managing COVID-19, the insights from this study can be generalized to improve preparedness for future pandemics. The SIR model’s adaptability to varying parameters makes it a robust tool for simulating different scenarios. Policymakers can use these simulations to design contingency plans, stockpile resources, and develop infrastructure to address potential crises more effectively. This proactive approach is essential for mitigating the impact of infectious diseases in a globalized world.
A critical gap often exists between scientific models and their application in policymaking. By presenting clear, data-driven insights, this study bridges that gap, enabling policymakers to base decisions on robust evidence. For instance, the model’s ability to quantify key parameters like the basic reproduction number (R0) and removal rates provides concrete metrics for evaluating the effectiveness of interventions. Such data can guide policies that balance public health needs with economic and social considerations. The study’s focus on three diverse countries—Thailand, Lithuania, and Belarus—demonstrates the model’s versatility across different contexts. By sharing methodologies and insights internationally, governments can foster collaboration to combat global health challenges. The adoption of similar models in regions with varying healthcare capacities and socio-economic conditions could lead to a more coordinated global response, particularly in resource-limited settings. The integration of predictive modeling into public health strategies has transformative potential. By providing actionable insights and supporting data-driven decision-making, the findings of this study contribute to more effective management of COVID-19 and lay a foundation for future applications in pandemic control.
Challenges and limitations
Although the classical SIR model serves as a foundational tool for capturing overarching pandemic trends, it relies on the simplifying assumption of homogeneous mixing, where all individuals are equally likely to interact and transmit the virus. This assumption does not fully reflect real-world heterogeneity, where factors such as population density, urban-rural differences, age structure, and mobility patterns contribute to variable transmission dynamics. Additionally, the model does not explicitly account for asymptomatic carriers, who play a significant role in COVID-19 transmission, nor does it incorporate the evolving impact of variants of concern, which demonstrate varying transmissibility and immune escape potential. Future extensions of this work could benefit from adopting more refined compartmental models, such as SEIR models, that explicitly include exposed and asymptomatic compartments, or agent-based simulations capable of capturing population-level heterogeneity. While such models offer enhanced realism, they also introduce greater complexity, requiring more granular data and computational resources. Balancing model simplicity with epidemiological realism remains a key challenge in pandemic modeling.
Notably, while the SIR model was originally developed to capture the dynamics of infectious disease outbreaks, its fundamental compartmental structure offers potential adaptability for modeling certain non-communicable health conditions at the population level. In the context of cardiovascular diseases, heart failure, or acute coronary syndromes, a modified SIR-like framework could theoretically classify individuals into compartments such as at-risk (susceptible), diagnosed (infected), and managed or stabilized (recovered). However, applying the SIR model to non-communicable diseases would require substantial modifications to account for chronic risk factors, progressive physiological deterioration, individualized treatment responses, and the prolonged time horizons characteristic of these conditions. Unlike infectious diseases, which typically involve short-term transmission dynamics, chronic diseases demand models that integrate lifestyle factors, genetic predispositions, environmental exposures, and the cumulative effects of medical interventions. Despite these challenges, the core strengths of compartmental modeling—its clarity, simplicity, and ability to describe population-level transitions—make it an attractive candidate for hybrid frameworks that merge epidemiological modeling with chronic disease surveillance and health systems data. Exploring these interdisciplinary applications could enhance both predictive modeling and long-term public health planning, particularly in understanding the cascading effects of public health crises, such as pandemics, on the incidence and progression of chronic diseases.
This study applied the SIR model to analyze COVID-19 dynamics in Lithuania, Belarus, and Thailand—three countries selected to capture varying pandemic responses and available data reliability. While the model demonstrated strong predictive performance in these cases, its broader applicability across nations with differing healthcare infrastructures, population densities, and pandemic policies warrants further investigation. The flexibility of the SIR framework allows parameter adjustments to account for context-specific factors, but successful adaptation requires recalibration using local epidemiological data. Future work will focus on expanding the model’s application to a more diverse set of countries, enabling a more comprehensive evaluation of its generalizability and robustness across different public health environments.
Moreover, while the SIR model successfully captured the overall COVID-19 trends in Lithuania, Belarus, and Thailand, it is important to acknowledge the inherent uncertainties associated with parameter estimation in real-time epidemic modeling. Factors such as underreported cases, variability in testing coverage, changes in population behavior, and evolving public health interventions contribute to substantial uncertainty in key model parameters, including transmission rates and recovery rates. Future extensions of this work will incorporate formal uncertainty quantification methods, such as Monte Carlo simulations and sensitivity analyses, to better assess the robustness of model projections and provide confidence intervals for key outputs. Such approaches would enhance the reliability of model-based forecasts and strengthen their utility for informing public health strategies under conditions of incomplete or evolving data.
Conclusion
Mathematical modeling theories play a pivotal role in the exploration of pandemics, particularly in the context of infectious diseases. These models are instrumental in guiding societies and decision-makers in implementing strategies to better combat widespread illnesses. This article focuses on the utilization of the SIR model, which, aside from its computational simplicity, furnishes vital and pertinent outcomes. It efficiently anticipates the trajectory of a disease, making it an indispensable tool. Simulations using mathematical modeling were conducted through MATLAB software to predict future patient numbers in three countries: Thailand, Lithuania, and Belarus. Additionally, the tally of recovered patients was determined using the MATLAB function ‘fminsearch’. By applying these models to real-time data from these countries, forecasts have been generated to indicate the points when the disease reaches its peak, effectively highlighting the ascending and descending patterns of the disease. Notably, while Thailand exhibits a drastic downward trend, the graphs for the other two countries illustrate consistent slopes, indicating the absence of widespread vaccination. The slight descent observed in specific instances suggests the enforcement of government-mandated quarantines in these countries.
Abbreviations
| COVID-19: | coronavirus disease 2019 |
| LSTM: | Long Short-Term Memory |
| RMSE: | root mean square error |
| SARS-CoV-2: | severe acute respiratory syndrome coronavirus 2 |
| SEIR: | Susceptible-Exposed-Infectious-Recovered |
| SIR: | Susceptible-Infectious-Recovered |
Declarations
Author contributions
ZS, MG, MF, and RS: Conceptualization, Writing—original draft. KR: Conceptualization, Writing—original draft, Writing—review & editing. FA: Formal analysis, Investigation, Data curation. HR: Writing—review & editing. All authors read and approved the submitted version.
Conflicts of interest
The authors declare that they have no conflicts of interest.
Ethical approval
This study utilized publicly available data from the Worldometer website, which contains aggregated and anonymized data on COVID-19 statistics. As the research does not involve human participants, identifiable data, or intervention, it did not require Institutional Review Board (IRB) approval or ethical clearance under the guidelines applicable to secondary data analysis.
Consent to participate
Not applicable.
Consent to publication
Not applicable.
Availability of data and materials
The datasets for this manuscript are not publicly available because the data was obtained from the Worldometer website. Requests for accessing the datasets should be directed to Dr. Zahra Shirmohammadi (shirmohammadi@sru.ac.ir).
Funding
Not applicable.
Copyright
© The Author(s) 2025.
Publisher’s note
Open Exploration maintains a neutral stance on jurisdictional claims in published institutional affiliations and maps. All opinions expressed in this article are the personal views of the author(s) and do not represent the stance of the editorial team or the publisher.
PDF
